Composition of Unshaped Refractory Particle Size

Controlling the size distribution (composition) is one of the most important measures to control the product quality in the preparation of amorphous refractories. Grain size distribution is reasonable or not, not only affects the operation performance of materials, such as rheology, plasticity, workability, spreadability, adhesion rate (or resilient rate), etc., but also affects the lining body made after the material physical properties, such as porosity, bulk density, permeability, mechanical strength, elastic modulus and so on, thus affecting the end-use properties of materials, such as thermal shock resistance, the permeability of the melt and erosion resistance, wear resistance and erosion resistance and structure strength under high temperature, etc.
Introduction to particle gradation theory
The particle size of amorphous refractory aggregate is provided with two forms: discontinuous (discontinuous) particle size accumulation and continuous particle size accumulation:
(1) discontinuous particle size accumulation is the accumulation of discontinuous particle size (which can be monodisperse particles of different particle sizes, or particles of different particle sizes with a narrow range of particle sizes).
(2) continuous particle size accumulation refers to the accumulation of particles distributed by continuous particle size.
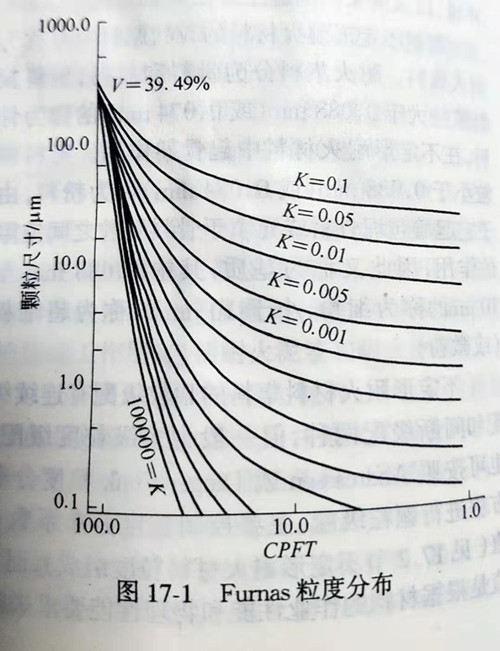
The theory of particle accumulation with discontinuous particle size was first proposed by Furnas. The theory holds that: the accumulation composed of several levels of particle size, such as the accumulation composed of three levels of particle size, in which the particles should be exactly filled into the gap formed by the accumulation of coarse particles, while the fine particles should be exactly filled into the gap formed by the accumulation of coarse particles, thus forming the most compact accumulation. If it is composed of multiple particle size, the porosity will be closer and closer to zero when finer and finer particles are added. However, when the particle size distribution is constituted, the number of particles at each level needs to form geometric series. Later, he extended the expression of multiple grains to the calculation of continuous distribution. The equation is as follows:
CPFT/100= (rlogd-rlogds) /(rlogdl-rlogds)...
Where, CPFT -- the cumulative percentage below a certain grain grade (D);
R -- the ratio of the number of particles of two adjacent particle sizes;
D -- particle size (size);
Ds -- minimum particle size;
DL - maximum particle size.
When the relationship between D and CPFT in the Furnas equation is plotted on the logarithmic coordinate axis (log-log graph), its grain size distribution is a curve distribution, as shown in FIG. 17-1. K=Ds/DL in FIG. 17-1.

The theory of continuous particle size accumulation was proposed by Andreassen. He proposed the particle distribution equation as follows:
CPFT / 100 = (D/DL) q...
Where, q is the particle size distribution coefficient, and the meanings represented by other symbols are the same as before. The grain size distribution curve is shown in figure 17-2.

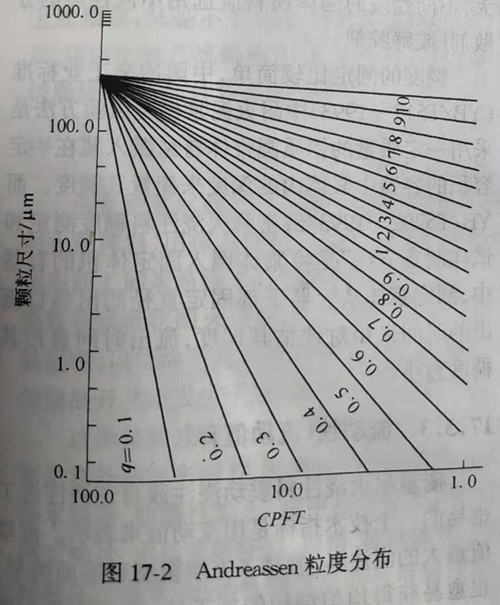
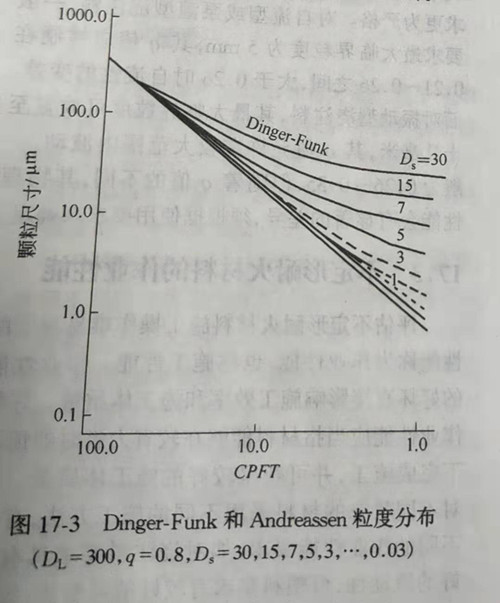
Comparison with the Furnas equation shows that there is no minimum particle size limit in the Andreassen equation, that is, the minimum particle size is unlimited, while the real particle size distribution is limited. Therefore, some people put forward different opinions on it. In order to deal with the problem of no minimum particle size limitation in the Andreassen equation, Dinger and Funk modified the Andreassen equation through mathematical reasoning and processing according to Furnas's finite distribution equation (with the limitation of maximum particle size DL and minimum particle size Ds) and proposed the dinger-funk equation:
CPFT / 100 = (Dq - Dqs)/(DLq - Dqs)...
It can be seen from equation (17-3) that Dinger-Funk equation is the same as Andreassen when Ds goes to 0. Figure 17-3 is a comparison diagram of the particle size distribution of Dinger-Funk and Andreassen, in which DL and q are constants. It can be seen that when Ds is smaller, the particle size distribution curves of the two equations are closer.
As can be seen from figure 17-3, the Dinger-Funk equation is plotted on the log-log axis with CPFT pair D, and its particle size distribution is curvilinear, close to the actual particle size distribution, but a little troublesome to calculate. When the Andreassen equation is plotted on the log-log axis with CPFT to D, the particle size distribution is a straight line, and the q value is the slope of the line, which is simple and easy to adopt.

Granularity composition control. 
The particle size composition of amorphous refractory varies with the different construction methods. In the past, coarse particles were generally divided into three grades: coarse particles (> 1.5mm), medium particles (1.5~0.074mm), and fine particles (less than 0.074mm). In the pellet composition of ramming construction materials, the coarse, medium and fine ratio is generally 40:30:30 (or 40:35.25), but now it tends to use multistage pellet gradation, and the pellet accumulation theory is used to guide the pellet gradation of amorphous refractory materials.
Andreassen particle size distribution equation is the most widely used in the preparation of amorphous refractory, and Dinger-Funk particle size distribution equation is also used if there is a minimum particle size limit, but no matter which equation is used, the most important is to control the particle size distribution coefficient q. According to the determined q value, the composition ratio of granularity in different particle size ranges is adjusted. The size of the q value is based on the performance (rheological) and performance requirements of the test to determine.
In the amorphous refractories, casting refractories is the most important requirement for the grading of particles. In the castable, artesian or pump-fed castables have more stringent requirements on particle gradation than vibrating castables. For artesian or pumped castable, the maximum critical particle size is generally required to be 5mm, and the q value should be controlled between 0.21 and 0.26, and the variation of artesian property should be greater than 0.26. For vibrating castables, the maximum critical particle size can be relaxed to more than 10 millimeters, and the q value is allowed to fluctuate in a wide range, generally 0.26~0.35, but with the difference of q value, its physical properties will have significant differences, which must be determined according to the use requirements.